解法：半枚举、动态规划。

首先是观察数据规模发现mm很小，于是可以在mm上做文章（这是我一直以为是状压DP的原因。。。）——将mm行的方向枚举出来，这样变量就只有nn列的方向了。

以下都是在mm行的方向确定情况进行的讨论。

然后对于一个要求（x1,y1）（x1,y1）、（x2,y2）（x2,y2），x1x1与x2x2，y1y1与y2y2关系确定，我们画图可以发现所有的情况都可以等效为一下4种（不包括x1=x2x1=x2或y1=y2y1=y2情况）：

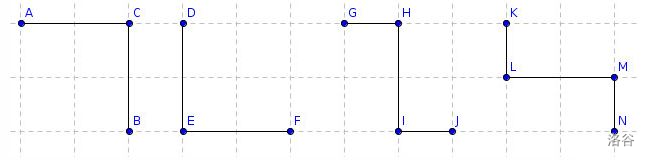
将其归纳一下，就是：

当x1x1行、x2x2行符合方向时，[y1,y2][y1,y2]列中要有一个符合方向。

当只有x1x1行符合方向时，yy列要符合方向。

当只有x2x2行符合方向时，y1y1列要符合方向。

当x1x1行、x2x2行都不符合方向时，y1y1、y2y2要同时符合方向。

然后讨论x1=x2或y1=y2的情况：

当x1=x2x1=x2且y1=y2y1=y2时，无论方向都符合。

当x1=x2x1=x2且y1<>y2y1<>y2时，x1x1行要符合方向。

当x1<>x2x1<>x2且y1=y2y1=y2时，y1y1列要符合方向。

因为x1x1、x2x2行的方向建立在半枚举的基础上，所以当不满足方向时，就是无效状态。

排除无效状态后，设SS为1，NN为0，将nn列的方向看作长度为nn的数字串，那么上面yy列的满足条件就都可以等价于区间[l,r][l,r]中要有一个为0或1。

设为0为0区间，为1为1区间。

问题就变成了求最小代价使所有0、1区间全部得到满足，于是可以用动态规划解决。

DP之前将所有的0、1区间讨论处理出来，分别按l为第一关键字，r为第二关键字排序，作为DP基础。

DP之前还有一个小小的剪枝，就是对于0、1性质相同的区间，如果存在包含关系，则去掉大区间，因为小区间满足大区间也肯定满足，这个优化的效果十分显著。

设cost[i,1]cost[i,1]表示把i列方向变成1的代价，对应的有cost[i,0]cost[i,0]。

动态规划的方程是f[i,j,k]f[i,j,k]表示前i−1i-1列状态确定，且满足了排序后的所有编号在[1,j−1][1,j-1]的0区间与所有编号在[1,k−1][1,k-1]的1区间的最小代价。

这样通过讨论第i列的状态，f[i,j,k]f[i,j,k]就可以转移到f[i,j1,k1f[i,j1,k1。其中若第i列方向为0，则j1j1为第一个左界>ii的0区间，k1k1为kk，转移时要加上cost[i,0]cost[i,0]；若第ii列方向为1，则j1j1为jj，k1k1第一个左界>ii的1区间，转移时要加上cost[i,1]cost[i,1]。

注意枚举还需要有左边界j0j0、k0k0代表第一个包含i的区间，而所有的右边界<ii的区间应该在枚举ii之前全部保证满足。因为没有左边界会从无效状态直接跳到j1j1、k1k1，漏掉很多区间限制。

每一个ii的j1j1与k1k1都可以预处理出来，这样递推取最小值就可以了。边界是f[1,1,1]=0f[1,1,1]=0，结果是f[n+1,sum[0]+1,sum[1]+1]+f[n+1,sum[0]+1,sum[1]+1]+当前行状态的生成代价

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <algorithm>
using namespace std;
const int maxn=111, maxl = 201, inf = 100000000;
int n, m, K, SM, SN[maxn], r[3], rr[3][maxn], ll[3][maxn], costm[maxn][3], costn[maxn][3];
int sm[maxn], sn[maxn], vm[maxn], vn[maxn], f[maxn][maxl][maxl], pp[maxn][maxl][maxl];
char s[maxn], tm[3], tn[3];
bool g[maxn][maxl][maxl];
struct req { int x1, x2, y1, y2; } a[maxn];
struct inter { int l, r; } in[3][maxl]; 

void init()
{
    scanf("%d%d", &m, &n);
    scanf("%s", s);
    for (int i=1; i<=m; ++i) sm[i] = (s[i-1]=='E');
    scanf("%s", s);
    for (int i=1; i<=n; ++i) sn[i] = (s[i-1]=='S');
    for (int i=1; i<=m; ++i) 
    {
        scanf("%d", vm+i);
        costm[i][sm[i]] = 0, costm[i][1-sm[i]] = vm[i];
    }
    for (int i=1; i<=n; ++i) 
    {
        scanf("%d", vn+i);
        costn[i][sn[i]] = 0, costn[i][1-sn[i]] = vn[i];
    }
    scanf("%d", &K);
    for (int i=1; i<=K; ++i) 
        scanf("%d%d%d%d", &a[i].x1, &a[i].y1, &a[i].x2, &a[i].y2);
    tm[0] = 'W', tm[1] = 'E', tn[0] = 'N', tn[1] = 'S';
}

inline bool cmp(const inter &a,const inter &b) 
{ return a.l<b.l || (a.l==b.l && a.r<b.r); }

void maintain()
{
    sort(in[0]+1,in[0]+r[0]+1,cmp);
    sort(in[1]+1,in[1]+r[1]+1,cmp);
    for (int q=0; q<2; ++q)
    {
        for (int i=1; i<=n; ++i)
        {
            int j = 1; ll[q][i] = 1;
            for (; j<=r[q]; ++j)
            if (in[q][j].l>i) break;
            else if (in[q][j].r<i) ll[q][i] = j+1;
            rr[q][i] = j; 
        }
    }
}

void add(int p, int L, int R)
{
    if (L>R) swap(L,R);
    for (int i=1; i<=r[p]; ++i)
        if (L<=in[p][i].l && in[p][i].r<=R) return;
    in[p][++r[p]].l = L, in[p][r[p]].r = R; 
}

bool prepare(int s)
{
    memset(rr, 0 ,sizeof rr);
    memset(ll, 0, sizeof ll);
    r[0] = 0, r[1] = 0;
    for (int i=1; i<=K; ++i)
    {
        int x1 = a[i].x1, y1 = a[i].y1, x2 = a[i].x2, y2 = a[i].y2;
        int p = (x1<x2), q = (y1<y2);
        if (x1!=x2 && y1!=y2)
        {
            if (((s >> (x1-1)) & 1)==q && ((s >> (x2-1)) & 1)==q) add(p,y1,y2); 
            else if (((s >> (x1-1)) & 1)==q) add(p,y2,y2);
            else if (((s >> (x2-1)) & 1)==q) add(p,y1,y1);
            else
            {
                int t = 0, fr=min(x1,x2)+1, en=max(x1,x2);
                for (int j=fr; j<en; ++j)
                    if (((s >> (j-1)) & 1)==q) t = 1;
                if (!t) return 0;
                add(p,y1,y1); add(p,y2,y2);
            }
        }
        else if (x1==x2 && y1!=y2 && ((s >> (x1-1)) & 1) != q) return 0;
        else if (x1!=x2 && y1==y2) add(p,y1,y2);
    }
    maintain();
    return 1;
}

int dp()
{
    memset(f, 0x7, sizeof f);
    f[1][1][1] = 0;
    for (int i=1; i<=n; ++i)
    for (int j=ll[0][i]; j<=rr[0][i]; ++j)
    for (int k=ll[1][i]; k<=rr[1][i]; ++k)
    if (f[i][j][k]<inf)
    {
        if (f[i+1][rr[0][i]][k]>f[i][j][k]+costn[i][0])
        {
            f[i+1][rr[0][i]][k] = f[i][j][k]+costn[i][0];
            g[i+1][rr[0][i]][k] = 0;
            pp[i+1][rr[0][i]][k] = j;
        }
        if (f[i+1][j][rr[1][i]]>f[i][j][k]+costn[i][1])
        {
            f[i+1][j][rr[1][i]] = f[i][j][k]+costn[i][1];
            g[i+1][j][rr[1][i]] = 1;
            pp[i+1][j][rr[1][i]] = k;
        }
    }
    return f[n+1][r[0]+1][r[1]+1];
}

void get_SN(int i, int j, int k)
{
    if (i==1) return;
    SN[i-1] = g[i][j][k];
    if (!g[i][j][k]) get_SN(i-1,pp[i][j][k],k);
    else get_SN(i-1,j,pp[i][j][k]);
}

void work()
{
    int tot = (1<<m), ans = inf;
    for (int i=0; i<tot; ++i)
    {
        int t = 0;
        for (int j=1; j<=m; ++j) t += costm[j][(i>>(j-1))&1];
        if (prepare(i))
        {
            t += dp();
            if (t<ans)
            {
                ans = t, SM = i;
                get_SN(n+1,r[0]+1,r[1]+1);
            }
        }
    }
    if (ans<inf)
    {
        printf("possible\n");
        printf("%d\n", ans);
        while (m--) printf("%c", tm[SM & 1]), SM >>= 1;
        printf("\n");
        for (int i=1; i<=n; ++i)printf("%c", tn[SN[i]]);
        printf("\n");
    } else printf("impossible\n");
}

int main()
{
    //freopen("manhattan.in", "r", stdin);
    //freopen("manhattan.out", "w", stdout);
    init();
    work();
    return 0;
}

虽然要枚举所有的mm行状态、nn列、sum[0]sum[0]、um[1]um[1]，理论极限时间复杂度是O（2mnk2）O（2^mnk^2），但是由于dp之前的排除大区间的优化，k2k^2实际上是远远达不到的，因为大部分的0、1区间长度都是1，所以不用担心超时的问题。